1. Задание № 264 

Сложность: III
Классификатор алгебры: 4\.1\. Уравнения первой и второй степени относительно показательных функций
Методы алгебры: Замена переменной
Показательные уравнения
i
Найдите сумму корней уравнения 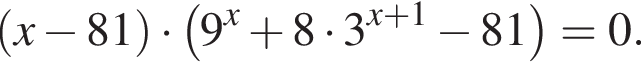
Решение. Рассмотрим уравнение 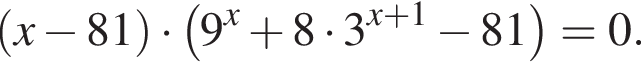 Оно имеет решение, когда выражение в одной из скобок равно нулю. Из первой скобки
Оно имеет решение, когда выражение в одной из скобок равно нулю. Из первой скобки 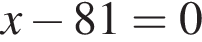 следует, что первый корень
следует, что первый корень  Рассмотрим
Рассмотрим 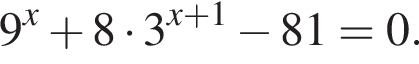 Сделаем замену
Сделаем замену  Тогда:
Тогда:

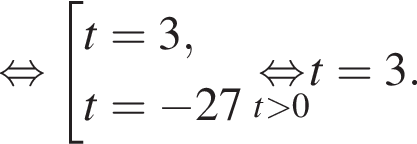

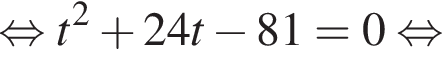
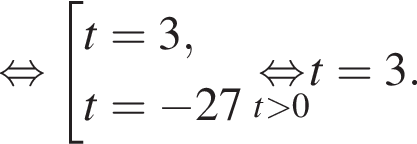
Вернемся к исходной переменной  Отсюда следует, что сумма корней уравнения равна 82.
Отсюда следует, что сумма корней уравнения равна 82.
Ответ: 82.
Ответ: 82
264
82
Сложность: III
Классификатор алгебры: 4\.1\. Уравнения первой и второй степени относительно показательных функций
Методы алгебры: Замена переменной
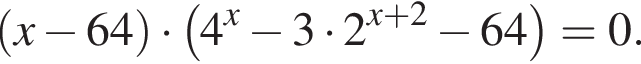
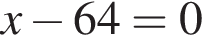 следует, что первый корень
следует, что первый корень  Рассмотрим
Рассмотрим 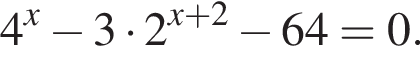 Сделаем замену
Сделаем замену 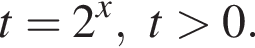 Тогда:
Тогда: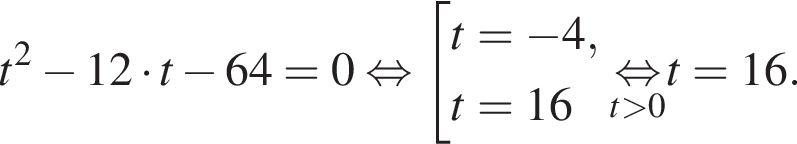
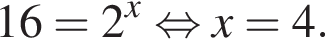 Отсюда следует, что сумма корней уравнения равна 68.
Отсюда следует, что сумма корней уравнения равна 68.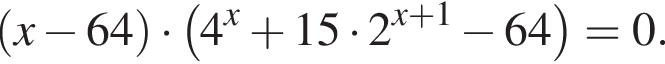
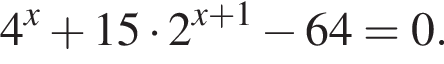 Сделаем замену
Сделаем замену 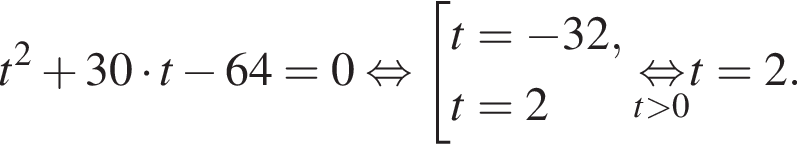
 Отсюда следует, что сумма корней уравнения равна 65.
Отсюда следует, что сумма корней уравнения равна 65.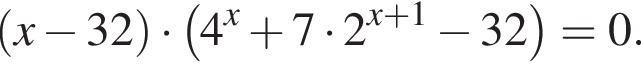
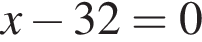 следует, что первый корень
следует, что первый корень 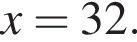 Рассмотрим
Рассмотрим 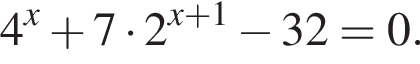 Сделаем замену
Сделаем замену 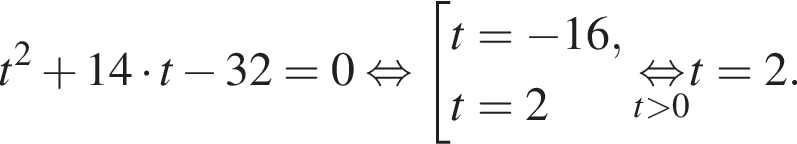
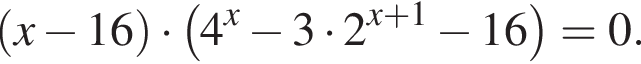
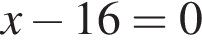 следует, что первый корень
следует, что первый корень 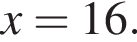 Рассмотрим
Рассмотрим 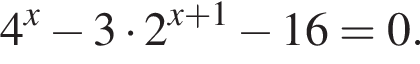 Сделаем замену
Сделаем замену 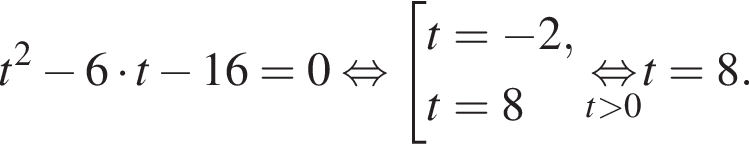
 Отсюда следует, что сумма корней уравнения равна 19.
Отсюда следует, что сумма корней уравнения равна 19.